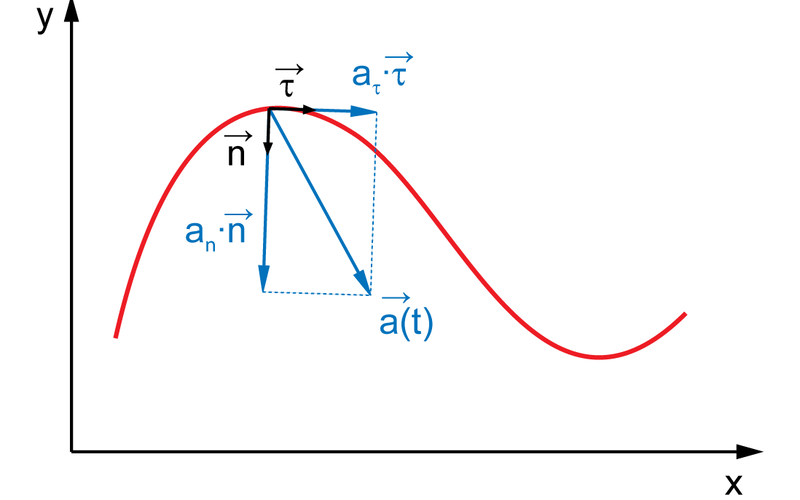
Может ли тело ускоряться, если оно движется с постоянной скоростью? Ага! Многие люди сначала находят это нелогичным, потому что забывают, что изменение направления движения объекта — даже если объект сохраняет постоянную скорость — по-прежнему считается ускорением.
Ускорение — это изменение скорости либо по величине , т. е. по скорости, либо по направлению , либо по тому и другому . При равномерном круговом движении направление скорости постоянно меняется, поэтому всегда есть соответствующее ускорение, даже если скорость может быть постоянной. Вы сами испытываете это ускорение, когда поворачиваете в своей машине — если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы находитесь в равномерном круговом движении. То, что вы замечаете, — это боковое ускорение, потому что вы и автомобиль меняете направление. Чем круче кривая и чем больше ваша скорость, тем более заметным станет это ускорение. В этом разделе мы рассмотрим направление и величину этого ускорения.
Вывод формулы центростремительного ускорения
На следующей диаграмме показано тело, движущееся по круговой траектории с постоянной скоростью.

Здесь направление центростремительного ускорения направлено к центру кривизны. Кроме того, вы должны отметить, что треугольники, созданные радиусами r, Δs и векторами скорости, одинаковы. Кроме того, треугольники PQR и ABC имеют две одинаковые стороны, что означает, что они равнобедренные треугольники. Более того, эти две одинаковые стороны треугольников вектора скорости являются скоростями v1 = v2 = v. Тогда, используя признаки двух равных треугольников, находится:
- Δv/v = Δs/r
Ускорение равно Δv / Δt, а решение для Δv:
- Δv = ( v / r )Δs
Далее, разделив на Δt,
- Δv / Δt = v / r × Δs / Δt
Итак, наконец, обратите внимание, что
Δv / Δt = a c , а Δs / Δt = v, тангенциальная или линейная скорость, величина центростремительного ускорения a c = v 2 / r
Итак, с помощью этого уравнения вы можете определить, что центростремительное ускорение более значимо на высоких скоростях и на кривых меньшего радиуса.
Примечание: единицей СИ для центростремительного ускорения является м/с2 .
Решенные числа
1. Камень, привязанный к веревке, движется с фиксированной скоростью 10,0 м/с по окружности радиусом 8,0 м. Оцените примерную величину центростремительного ускорения породы.
Решение. По формуле a c = v 2 / r
Следовательно, а с = (10) 2 / 8
а с = 12,5 м/с 2
2. В случае набора игровых автоматов его максимальное центростремительное ускорение без выброса с гусеницы составляет 3,8 метра в секунду в квадрате. Замечено, что эти игровые автоматы слетают с трассы, когда их скорость превышает 1,1 метра в секунду. Каков радиус кривой на треке? Ответ в метрах.
Решение. Максимально возможное центростремительное ускорение равно а = 3,8 м/с 2 , а максимальная скорость, которую могут развивать эти игровые автомобили, не слетая с пути, составляет 1,1 м/с.
Применяя эту формулу центростремительного ускорения, получаем ответ:
а с = v 2 / г
Следовательно, r = v 2 / a c
= (1,1 м/с) 2 / 3,8 м/с 2
= 0,32 м